Ok, here's the highest exponent base I can get so far:
O(168151n)EDIT: Lurker allows infinite coins, but if I take lurker and hunting grounds out of the kingdom and just use stonemason, I get
O(65536n)Kingdom: Bridge, Fortress, Possession, Golem, Alchemist, Scrying Pool, Stonemason, King's Court, Hunting Grounds, Lurker
Events: Inheritance, Training
Setup: Inherit King's Court, train King's Court.
Hand: Fortress, Scrying Pool, 2x King's Court, Lurker, 2x Stonemason, n - 7 Possessions
Turn: Kc-Kc-Lurker-SM-SM, trashing 3 hunting grounds for 9 estates, 5 fortresses for 2 lurkers and 8 stonemasons, and one Possession for a golem and a scrying pool. Play scrying pool, draw it all.
7x Kc on: 2 lurkers to get 18 more Kc, 8 stonemasons for 33 more stonemasons, and 13 more lurkers, and a pool and an alchemist from the golem, then draw them all with pool. Now I have ~40 spare KC plays...
...and so on. The general plan is:
Have n KC plays, ~3n/4 stonemasons, ~n/4 lurkers. Get ~9n/4 KCs from the lurkers. The stonemasons give 9n/2 gains, which I use for ~27n/8 stonemasons and ~9n/8 lurkers. If I have one scrying pool in hand, trash an alchemist for two scrying pools. If I have two scrying pools in hand and no alchemists, trash a golem for two alchemists. If I have two scrying pools and an alchemist but no golem, then trash a possession for two golems. Otherwise, don't bother. Then play a scrying pool.
I now have ~9n/2 KC plays and the correct proportion of stonemasons and lurkers. Repeat. In the end, I get to play 8n - 60 scrying pools (After the first few rounds, I will be getting the full 8 pools from each possession), and each time the number of King's Courts multiplies by 4.5 . I lose a little bit by forced inefficiencies and having to stonemason for pools sometimes, but that won't effect much. So I can get at least
O(4.58n - 60) ~ O(168151n) KC plays and so that many coins too.
My original plan was more complicated than this and involved develop lots of other crazy stuff, but I doubt it would have done much better. I bet this can still be very significantly improved though. I like how this just mainly uses lurkers, stonemasons, and estates, which all cost

. Also, is the number of different cards in the kingdom a limitation? I was at one point considering setting up a ridiculous number of cards in the trash that would be an exponential function of n before starting for lurker to get... would this be allowed?
The base of the exponent here is 4.58, because I can get ~8n pools and 4.5 gains/card. In particular, 12 cards (4 KCs, 6 SMs, and 2 lurkers) can gain 54 cards (18 KCs, 27 SMs, and 9 lurkers)... is it possible to improve this ratio or the number of pools? I guess we just need a card costing 
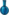
The title of this thread is interesting... I don't think busy beaver will be exactly attainable here...